| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- CI
- builder-pattern
- k8s
- Di
- java
- hibernate
- SpringMVC
- DevOps
- cd
- programmers
- IntelliJ
- 코딩테스트연습
- superBuilder
- dabase
- Oracle
- Kubernetes
- JPA
- docker
- CKA
- 해시맵
- 프로그래머스
- CI/CD
- map
- vuejs
- 뷰
- 알고리즘
- 자바
- Spring
- Vue
- ORM
- Today
- Total
문홍의 공부장
[Java] 프로그래머스 Lv.1 소수 찾기 풀이 : 에라토스테네스의 체(소수 구하기 알고리즘) 본문
소수 구하기 문제라고 가볍게 생각했다가, 효율성 테스트에서 시간초과를 맞고 띠용해서 찾으며 공부한 소수 구하는 알고리즘.
에라토스테네스의 체라는 알고리즘을 이번에 처음 접했다. 이름만 들어도 고대 그리스 수학자 느낌이 물씬 느껴진다..
문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한 조건
n은 2이상 1000000이하의 자연수입니다.
풀이 1. 자기 자신보다 작은 수로 나누어본다. 나누어 떨어지면 소수가 아니다.
가장 기본적인 방법. 입력받은 수 n 까지 반복문을 돌리며 소수를 찾아 flag 값을 바꾼다.
자기 자신(i)보다 작은 수(j)로 나누어 하나라도 나누어지는 수가 있으면 소수가 아니다. (아래 풀이에서 n = 30000 이다.)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public int solution(int n) {
int answer = 0;
boolean flag = true;
for (int i = 2; i <= n; i++) {
for (int j = 2; j < i; j++) {
if(i % j == 0) {
flag = false;
}
}
if(flag == true) answer++;
flag = true;
}
return answer;
}
|
cs |

풀이 2. 풀이1에서 불필요한 반복을 줄인다
풀이1 에서는, i % j 가 0이라는 것을 확인한 뒤에도 끝까지 반복문을 돌고 있다. break; 문을 추가함으로써 불필요한 반복 작업을 줄이고, 시간을 크게 단축할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public int solution(int n) {
int answer = 0;
boolean flag = true;
for (int i = 2; i <= n; i++) {
for (int j = 2; j < i; j++) {
if(i % j == 0) {
flag = false;
break;
}
}
if(flag == true) answer++;
flag = true;
}
return answer;
}
|
cs |

풀이 3. 소수들로만 나누어본다. 나누어 떨어지면 소수가 아니다.
소수 구하기 알고리즘은 규칙을 가지고 있다.
9는 3의 배수이다. 3은 소수이다.
10은 2, 5의 배수이다. 2,5는 소수이다.
14는 2, 7의 배수이다. 2, 7은 소수이다
=> 입력받은 수보다 작은 수의 소수들로 나누어 떨어지면 소수가 아니다 (소수의 배수는 소수가 아니다)
이를 위해 먼저 list에 가장 작은 소수(2)를 넣어두고, 반복문을 돌리며 소수로 나누어 떨어지는지 여부를 확인한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public int solution(int n) {
int answer = 0;
List<Integer> list = new ArrayList<Integer>();
list.add(2);
for (int i = 2; i <= n; i++) {
for (int j = 0; j < list.size(); j++) {
if(i % list.get(j) == 0) break;
if(list.size() == j+1) list.add(i);
}
}
return list.size();
}
|
cs |

풀이 4. 에라토스테네스의 체

풀이3에서 발전한 것이 에라토스테네스의 체이다. 풀이3에서 '소수의 배수는 소수가 아니다'라는 것을 알아냈다.
이를 다르게 정리하면, n까지의 수 중에서 소수를 찾는다고 할 때, n의 제곱근보다 작거나 같은 소수의 배수는 모두 소수가 아니다.
ex) n = 100일 때, √100 보다 작은 소수(2, 3, 5, 7) 의 배수는 모두 소수가 아니다.
정수 배열에 2부터 n까지의 수를 모두 넣어둔다. 그런 다음 n의 제곱근만큼 반복문을 돌리며 해당 수(i)의 배수(j)는 소수가 아니므로, 값을 0으로 바꾼다. 불필요한 반복을 피하기 위해 이미 값이 0으로 치환되었다면 continue; 를 통해 다음으로 넘어가도록 한다.
이후 배열에서 0이 아닌 값만을 카운트하면 소수의 개수를 구할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public int solution(int n) {
int answer = 0;
int[] arr = new int[n+1];
arr[0] = arr[1] = 0;
for (int i = 2; i <= n; i++) { arr[i] = i; }
for (int i = 2; i <= (int)Math.sqrt(n); i++) {
if(arr[i] == 0) continue;
for (int j = i+i ; j <= n; j+=i) { arr[j] = 0; }
}
for (int i = 0; i < arr.length; i++) {
if(arr[i] != 0) answer++;
}
return answer;
}
|
cs |
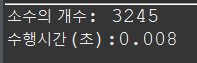
수행시간을 월등하게 단축시키는 모습을 확인할 수 있다.
References:
https://eblee-repo.tistory.com/27
https://marobiana.tistory.com/89
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [Java] 프로그래머스 Lv.1 문자열 내림차순으로 배치하기 풀이 (0) | 2020.02.06 |
|---|---|
| [Java] 프로그래머스 Lv.1 문자열 다루기 기본 풀이 (0) | 2020.02.06 |
| [Java] 프로그래머스 Lv.1 문자열 내 p와 y의 개수 풀이 (0) | 2020.02.06 |
| [Java] 프로그래머스 Lv.1 두 정수 사이의 합 풀이 (0) | 2020.02.03 |
| [Java] 프로그래머스 Lv.1 같은 숫자는 싫어 풀이 (0) | 2020.01.27 |
